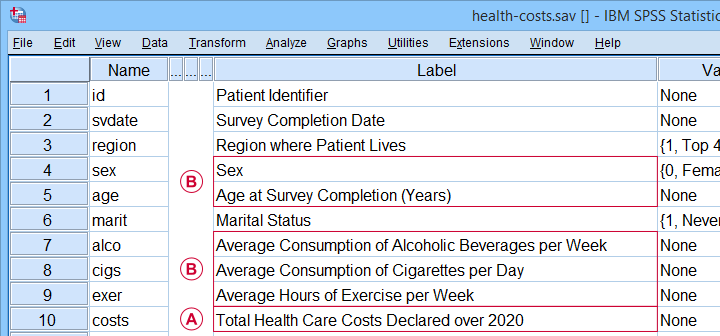
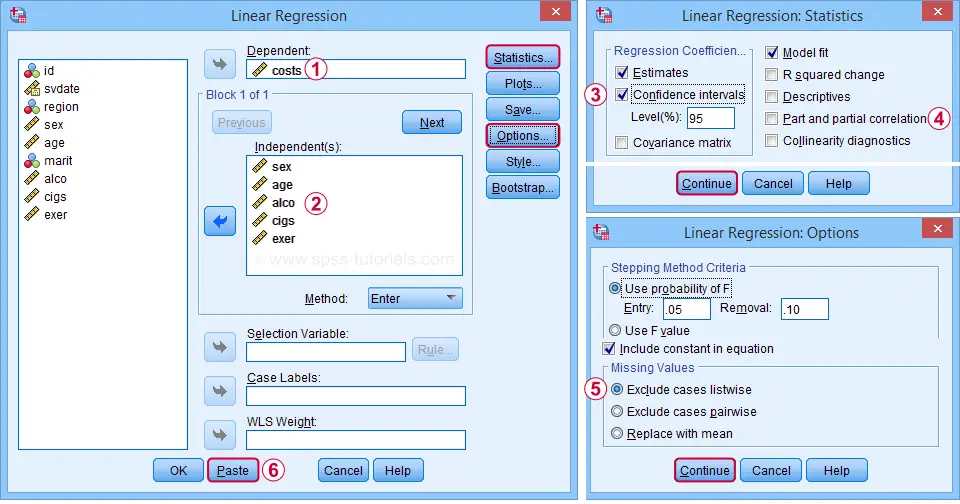
Một nhà khoa học muốn biết liệu chi phí chăm sóc sức khỏe có thể được dự đoán từ một số đặc điểm của bệnh nhân hay không và như thế nào. Tất cả dữ liệu đều có trong Health-Cost.sav như được hiển thị bên dưới.
Biến phụ thuộc là chi phí chăm sóc sức khỏe (tính bằng đô la Mỹ) được công bố trên năm 2020 hay gọi tắt là “chi phí”.
Các biến độc lập là giới tính, tuổi, uống rượu, hút thuốc và tập thể dục.
Nhà khoa học của chúng tôi cho rằng mỗi biến độc lập có mối quan hệ tuyến tính với chi phí chăm sóc sức khỏe. Do đó, ông quyết định phù hợp với mô hình hồi quy nhiều tuyến tính. Mô hình cuối cùng sẽ dự đoán đồng thời chi phí từ tất cả các biến độc lập.
Kiểm tra dữ liệu và thống kê mô tả
Trước khi chạy nhiều hồi quy, trước tiên hãy đảm bảo rằng
biến phụ thuộc là định lượng;
mỗi biến độc lập là định lượng hoặc phân đôi;
bạn có đủ kích thước mẫu.
Kiểm tra trực quan dữ liệu của chúng tôi cho thấy rằng các yêu cầu 1 và 2 được đáp ứng: giới tính là một biến phân đôi và tất cả các biến có liên quan khác đều là định lượng. Về kích thước mẫu, nguyên tắc chung là bạn muốn.
sử dụng ít nhất 15 quan sát độc lập
cho mỗi biến độc lập
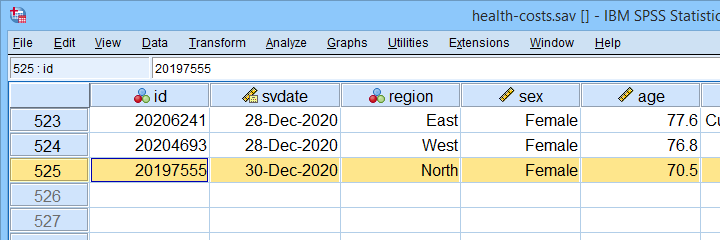
bạn sẽ bao gồm. Trong ví dụ của chúng tôi, chúng tôi sẽ sử dụng 5 biến độc lập vì vậy chúng tôi cần kích thước mẫu ít nhất là N = (5 · 15 =) 75 trường hợp. Dữ liệu của chúng tôi chứa 525 trường hợp nên điều này có vẻ ổn.
Tuy nhiên, hãy nhớ rằng chúng tôi không thể sử dụng tất cả các trường hợp N = 525 nếu có bất kỳ giá trị nào bị thiếu trong các biến của chúng tôi.
Bây giờ chúng ta hãy tiến hành một số kiểm tra dữ liệu nhanh. Tôi đặc biệt khuyến khích bạn ít nhất chạy biểu đồ cơ bản trên tất cả các biến. Kiểm tra xem phân bố tần số của chúng có hợp lý không. Có bất kỳ ngoại lệ nào không? Bạn có nên chỉ định bất kỳ giá trị bị thiếu nào không
kiểm tra biểu đồ phân tán cho mỗi biến độc lập (trục x) so với biến phụ thuộc (trục y). * Bạn có thấy bất kỳ quan hệ đường cong hoặc bất kỳ điều gì bất thường không?
chạy thống kê mô tả trên tất cả các biến. Kiểm tra xem có biến nào bị thiếu giá trị nào không và -nếu có- là bao nhiêu.
kiểm tra các mối tương quan Pearson giữa tất cả các biến. Tương quan tuyệt đối vượt quá 0,8 hoặc lâu hơn có thể gây ra các biến chứng (được gọi là đa cộng tuyến) cho phân tích hồi quy thực tế.
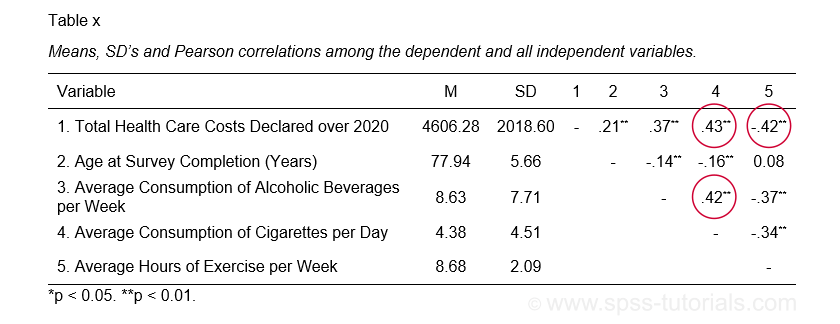
APA khuyên bạn nên kết hợp và báo cáo hai bảng cuối cùng này như được hiển thị bên dưới.
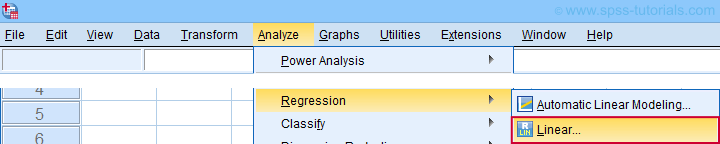
Những kiểm tra dữ liệu này cho thấy dữ liệu ví dụ của chúng tôi trông hoàn toàn ổn: tất cả các biểu đồ đều hợp lý, không có giá trị nào bị thiếu và không có mối tương quan nào vượt quá 0,43. Bây giờ chúng ta hãy tiến hành phân tích hồi quy thực tế.


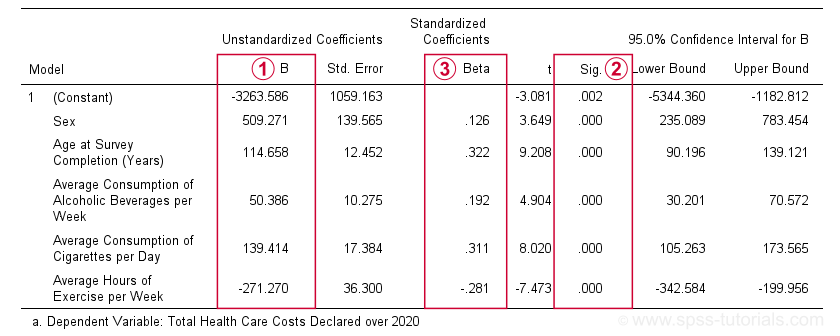
Hệ số b quy định mô hình hồi quy của chúng tôi:
Chi phí ′ = - 3263,6 + 509,3⋅Sex + 114,7⋅ Tuổi + 50,4⋅Alcohol + 139,4⋅ Thuốc lá điếu − 271,3⋅
trong đó Chi phí ′ biểu thị chi phí chăm sóc sức khỏe hàng năm được dự đoán bằng đô la.
Mỗi hệ số b cho biết mức tăng trung bình của chi phí liên quan đến mức tăng 1 đơn vị trong một yếu tố dự đoán. Ví dụ, độ tuổi tăng lên trong 1 năm dẫn đến chi phí tăng trung bình $ 114,7. Hoặc tăng 1 giờ tập thể dục mỗi tuần có liên quan đến mức tăng - $ 271,3 (tức là giảm $ 271,3) trong chi phí sức khỏe hàng năm.
Bây giờ, hãy nói về tình dục: tình dục tăng 1 đơn vị dẫn đến chi phí trung bình tăng 509,3 đô la. Để hiểu điều này có nghĩa là gì, xin lưu ý rằng giới tính được mã hóa là 0 (nữ) và 1 (nam) trong dữ liệu ví dụ của chúng tôi. Vì vậy, đối với biến này, mức tăng 1 đơn vị duy nhất có thể là từ nữ (0) lên nam (1). Do đó, B = $ 509,3 đơn giản có nghĩa là
chi phí trung bình hàng năm cho nam giới
cao hơn $ 509,3 so với nữ
(nghĩa là mọi thứ khác bằng nhau). Điều này hy vọng làm rõ cách các biến phân đôi có thể được sử dụng trong hồi quy bội. Chúng tôi sẽ mở rộng ý tưởng này khi chúng tôi sẽ đề cập đến các biến giả trong hướng dẫn sau.
Chữ "Sig." cột trong bảng hệ số của chúng tôi chứa giá trị p (2 đuôi) cho mỗi hệ số b. Như một hướng dẫn chung,
hệ số b có ý nghĩa thống kê nếu "Sig." hoặc p <0,05.
Do đó, tất cả các hệ số b trong bảng của chúng tôi đều có ý nghĩa thống kê cao. Chính xác, giá trị p là 0,000 có nghĩa là nếu một số hệ số b bằng 0 trong tổng thể (giả thuyết rỗng), thì có xác suất 0,000 để tìm thấy hệ số b mẫu quan sát được hoặc một hệ số cực đoan hơn. Sau đó, chúng tôi kết luận rằng hệ số b của tổng thể có lẽ không phải bằng 0.
Bây giờ, hệ số b của chúng ta không cho chúng ta biết sức mạnh tương đối của các yếu tố dự đoán của chúng ta. Điều này là do chúng có quy mô khác nhau: một điếu thuốc mỗi ngày nhiều hơn hay ít hơn một đồ uống có cồn mỗi tuần? Một cách để giải quyết vấn đề này là so sánh các hệ số hồi quy chuẩn hóa hoặc hệ số beta, thường được ký hiệu là β (chữ Hy Lạp “beta”). *
Hệ số beta (hệ số hồi quy chuẩn hóa) rất hữu ích để so sánh sức mạnh tương đối của các yếu tố dự báo của chúng tôi. Như vậy, 3 yếu tố dự đoán mạnh nhất trong bảng hệ số của chúng tôi là:
tuổi (β = 0,322);
tiêu thụ thuốc lá (β = 0,311);
bài tập (β = -0,281).
Hệ số beta thu được bằng cách chuẩn hóa tất cả các biến hồi quy thành điểm số z trước khi tính toán hệ số b. Việc chuẩn hóa các biến áp dụng một tiêu chuẩn (hoặc thang đo) tương tự cho chúng: điểm số z kết quả luôn có giá trị trung bình là 0 và độ lệch chuẩn là 1.
Điều này được duy trì bất kể chúng được tính toán qua nhiều năm, thuốc lá hay đồ uống có cồn. Vì vậy, đó là lý do tại sao các hệ số b được tính toán trên các biến chuẩn hóa - hệ sốbeta- có thể so sánh được trong và giữa các mô hình hồi quy.




Không có nhận xét nào:
Đăng nhận xét